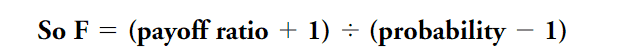Kelly’s formula for calculating capital in a transaction.
Kelly formula for bets is a universal approach for identifying the capital size both in gambling and exchange trading. We will speak about it in this article. Read in this article:
- Who Kelly is and how his famous formula came to life.
- What traders used the Kelly formula in trading and what the result was.
- Calculation technique, advantages and disadvantages.
- Kelly formula improvements.
Introduction
Beginner traders often think that a bigger risk results in a bigger potential profit. It makes sense but there is a nuance. In fact, the relation between the profit and risk is nonlinear.
Let’s assume that some trading strategy allows making USD 2 profit with the maximum USD 1 loss. The startup capital is USD 100 and there is a series of 40 trades. How much should be put at risk in order to get the maximum possible gain?
If you put too little at risk, you will fail to use the advantages of the positive mathematical expectation. If you put too much at risk, you can lose everything.
The Kelly formula can help you to calculate the optimum number of lots, which it makes sense to put at risk in every specific trade. The result will be objective if the decision about the number of lots is mathematically justified.
We will not dig into complex mathematical calculations but will give a general idea about the Kelly formula. If you find this article insufficient, you can read the book by Ralph Vince ‘The Mathematics of Money Management: Risk Analysis Techniques for Traders’.
A bit of history
In 1956, John Kelly, junior physicist from the Bell laboratory, wrote the ‘A New Interpretation of Information Rate’ article, in which he presented calculations of how a man, who has insider information about a win in a baseball game, should put a stake on.
The gambler increased his bet when chances on a win were high and decreased it when chances were low. Kelly limited the bet size and assumed that the maximum risk is acceptable only when the win probability was 100% – this is a rare situation but theoretically possible. In fact, Kelly described the optimum bet system – how to bet so that the money would only grow exponentially without a risk of losing the capital.
Later, the Kelly formula was adapted by Edward Thorp. In 1961 he wrote the ‘Fortune’s Formula: A Winning Strategy for Blackjack’ book.
What mathematical expectation and risk management are
The main trader’s task is to find such trades, the yield of which is higher than risk, besides a series of trades should have a positive mathematical expectation.
As soon as a good entry point appears, the trader decides what percentage of the capital he would put in a specific trade. More money should be put in more profitable trades for maximum profitability.
Mathematical expectation of the trading system is an average amount, which a trader can make or lose in each trade. See Picture 1.
Mathematical expectation
where P = probability of a win or loss;
A= made or lost amount;
N = number of possible results.
For example, Vince considers a USD 1 bet on a specific number in the roulette. In general, there are 38 numbers on the wheel, that is why mathematical expectation will look as follows:
(1 / 38 * USD 35) + (37 / 38 * (- USD 1)) = – 0.0526
In other words, if you place a bet of USD 1 on a number in the roulette, you can expect a loss of USD 5.62 in an average for one round. If you place USD 5, the loss will be 5 times bigger (USD 26.3).
If you trade with a negative mathematical expectation, there is no capital management scheme, which would result in a profit. That is why, in the long run, you can expect a profit only with a strategy that has a positive mathematical expectation. Moreover, it is not important how profitable the trading system is, because the results could be improved through capital management and selection of the number of traded contracts or lots.
Capital management is a decision making strategy for a maximum increase of the potential income with respect to the possible risk. Ideally, traders always hope for the better but should be prepared for the worse.
Vince specifies false concepts, which intraday traders often use:
- the higher the risk, the more you can make, which means that there is a linear relation between the profit and risk. (In fact, dependence of profit on risk is expressed as a curve with one peak, that is why the higher risk doesn’t increase the potential profit).
- Prices are rational.
- Risk calculation depends on the instrument, traded by a trader.
- Diversification decreases losses. (Actually, it reduces losses indeed, but only to a certain size).
Kelly formula for bets
The first Kelly equation looked as follows:
f = P – Q
where:
f – the capital share;
P – probability of the winning bet;
Q – probability of the loss, that is Q=1-P.
This formula could be applied if wins and losses are equal. If the win differs from the loss, the formula will not produce a correct result, that is why you shouldn’t use it for trading. This formula is, most often, applied for bets.
If the win and loss are not equal, you can use another variant:
f = ((B+1)*P-1)/B
where:
f – the start-up capital share;
P – the probability of the winning bet or trade;
B – the ratio of winning trades with respect to the loss-making trades.
Let’s assume that the gambler can make USD 1.5 with 60% probability and lose USD 1 with 40% probability. Then the optimum bet size could be calculated as follows:
f=((1.5+1)*0.6-1)/1.5=0.33
Which means that the gambler will get the biggest profit if he makes a bet equal to 33% of his start-up capital.
However, both these formulas could be applied only to the situations with the Bernoulli distribution, when only two outcomes are possible – a win or a loss.
What HPR, TWP and optimal f for traders are in Ralph Vince writings
Ralph Vince wanted to improve the Kelly formula for trading and calculate mathematically what amount should be put into a trade depending on the expected yield. That is, he wanted to find (for each market system) an optimal number of contracts or lots, which should be traded with a certain account balance in order to maximise the capital growth. This number of contracts or lots is the optimal f.
Vince added new concepts:
- HPR (holding period returns) is the rate of return for any trade + 1. That is, the number is >1 for profitable trades and – <1 for loss-making ones. For example, 10% profit will be considered as 1.1, while 25% loss will be considered as 0.75. HPR should be calculated for every trade:
HPR = 1 + f * (-T / BL)
F – the fixed capital share;
T – profit/loss in a trade with the opposite sign, which means that the loss becomes a positive number while profit becomes a negative number.
BL – the biggest loss in a series is always a negative value.
- TWP (terminal wealth relative) is the aggregate income of the trader trades in the form of an accumulation factor, that is multiplication of all HPR.
For example, TWP=15.69 means that the start-up capital was increased 15.69 times.
While looping f in the range from 0.1 to 1, you may find the number, which will produce the highest TWP for the trading system. It could be done in Excel.
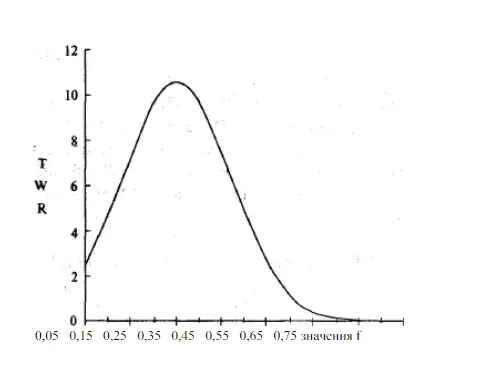
Optimal f allows to get the maximum profit when trading with a fixed capital share because the relation between the number of contracts and the win is a curve with one peak. It is not profitable to trade a very small number of contracts, because the potential profit will not be the maximum one. See Picture 2.
Vince pays special attention to the fact that it is important to give consideration to the general value of contracts rather than collateral margin, because the profit is calculated based on the general value of contracts and not on collateral margin. Moreover, there is a separate calculation for the profit reinvestment – you can find it in Vince’s book.
How to calculate the position size
So, the order of actions for calculating the optimal number of contracts or lots is the following:
- Take the history of the trading system trades with a positive mathematical expectation. A separate calculation has to be done for every trading system.
- Loop the possible f values from 0.1 to 1, inserting them into the TWP calculation formula. The highest TWP value will be with the optimal f value. The optimal f could be transformed into the money equivalent, for which you should divide the maximum loss by the negative f value.
- Calculate the geometrical mean for the trading system – it is the N-th root from TWP where N is a number of trades. You can compare various systems between themselves with the help of the geometrical mean.
Disadvantages of the optimal F calculation
- You might need a bigger number of contracts than it is possible in a specific market.
- The calculated number could be a fractional number and you will need to round it off.
- If stop losses are based on volatility or such technical indicators as Bollinger Bands, you will not be able to calculate the maximum loss.
- Distribution of series of loss-making and profitable trades very strongly influences the result.
- The number of contracts could be doubled for several trades. This could result in a huge drawdown in the event of an unsuccessful trade.
What famous traders used the Kelly formula
A modification of the Kelly formula was used by Larry Williams during the World Cup Championship of Futures Trading in 1987. He set the record at that championship, which hasn’t been broken yet and made 11,376% of yield on his trading account. See Picture 3.
This is the same formula we gave at the very beginning of the article – it is just written differently. Williams gives the following example:
Let’s assume that the system brings profit in 40% of cases and the reward:risk ratio is 2.5:1. In such a case the optimal variant is to trade with 16% of the capital.
f=((2.5+1)*0.4-1)/2.5=0.16
If the same system brings profit in 63% of cases, you already can trade with 48% of the capital.
f=((2.5+1)*0.63-1)/2.5=0.48
Williams increased and decreased the number of traded lots by this formula. Already in April he traded, in the average, 50 lots of Treasury Notes, he increased this number up to 237 by July and made a huge loss in this trade.
Summary
Excessive aspiration to increase the trading result by a profitable trading system could play a joke on you. Before you make high bets, make sure that your strategy produces a positive outcome in the long run. Study on historic data how many loss-making trades it can bring and open your positions in such a way so as to avoid irreparable losses. The ATAS platform will help you in it – its servers keep the detailed trading history on the most popular exchange instruments for many years.
Information in this article cannot be perceived as a call for investing or buying/selling of any asset on the exchange. All situations, discussed in the article, are provided with the purpose of getting acquainted with the functionality and advantages of the ATAS platform.